【每日算法Day 80】区间的并集与交集

LeetCode 56. 合并区间 (opens new window)

题目描述

给出一个区间的集合，请合并所有重叠的区间。

示例

输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6]

解题思路

首先将这些区间按照开始位置排序，并用两个变量left和right记录已知重叠区间的左右边界。接下来依次处理剩余要的区间interval[i]：

• 如果其左边界小于已知的右边界，则更新合并区间的右边界；
• 如果其左边界大于已知的右边界，则说明一个完整的重叠区间的合并已经完成，添加到结果集中并更新left和right为当前interval[i]的左右边界；

最后，还需要再执行一次添加到结果集的操作。

public int[][] merge(int[][] intervals) {
    if (intervals == null || intervals.length == 0) return new int[0][0];
    Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
    ArrayList<int[]> merged = new ArrayList<>();
    int left = intervals[0][0], right = intervals[0][1];
    for (int[] interval : intervals) {
        if (interval[0] <= right) {
            right = Math.max(right, interval[1]);
        } else {
            merged.add(new int[]{left, right});
            left = interval[0];
            right = interval[1];
        }
    }
    merged.add(new int[]{left, right});
    return merged.toArray(new int[0][]);
}

LeetCode 986. 区间列表的交集 (opens new window)

题目描述

给定两个由一些 闭区间 组成的列表，每个区间列表都是成对不相交的，并且已经排序。

返回这两个区间列表的交集。

（形式上，闭区间 [a, b]（其中 a <= b）表示实数 x 的集合，而 a <= x <= b。两个闭区间的交集是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3]。）

示例

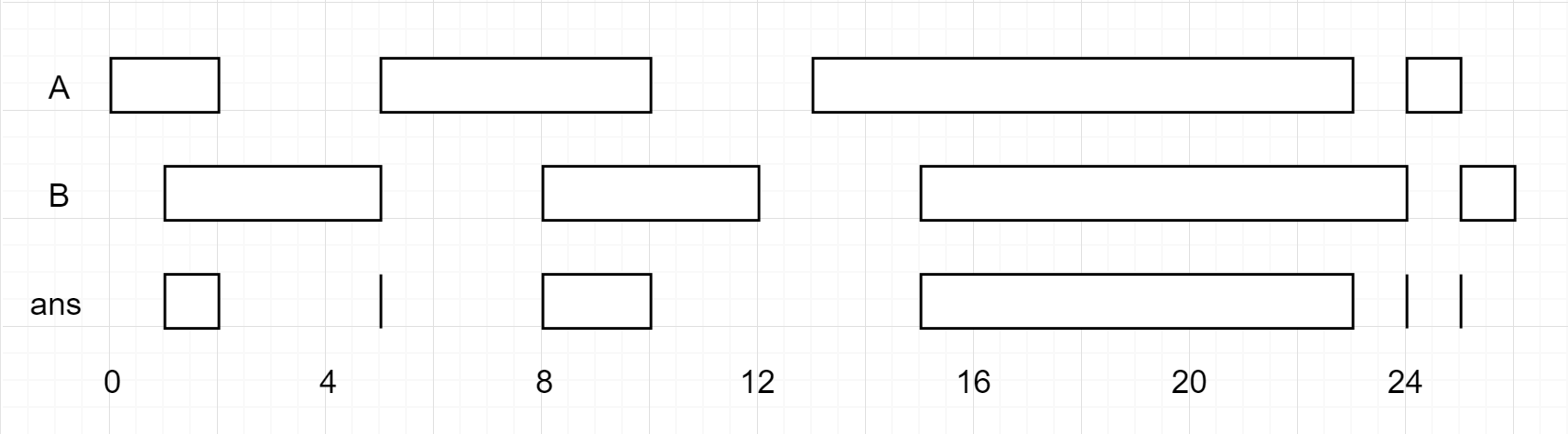
输入：A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
输出：[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

解题思路

判断两个区间是否有交集的标准是，记两个区间的左右边界分别为aL、aR、bL、bR：

• 如果aR<bL||bR<aL那么不存在交集
• 反之如果aR>=bL&&bR>=aL则存在交集，交集的左边界为max(aL,bL)，右边界为min(aR,bR)。

使用双指针来轮流比较两个列表中的区间，每次比较完毕后，需要选择下一个来比较的区间。显然应该选择二者中右边界更小的那一个的后面一个，因为后面一个可能和右边大的那个有交集。

public int[][] intervalIntersection(int[][] A, int[][] B) {
    if (A == null || A.length == 0 || B == null || B.length == 0) return new int[0][];
    int indexA = 0, indexB = 0;
    ArrayList<int[]> intersections = new ArrayList<>();
    while (indexA < A.length && indexB < B.length) {
        int aL = A[indexA][0], aR = A[indexA][1];
        int bL = B[indexB][0], bR = B[indexB][1];
        if (aR >= bL && bR >= aL) {
            intersections.add(new int[]{Math.max(aL, bL), Math.min(aR, bR)});
        }
        if (aR < bR)
            indexA++;
        else
            indexB++;
    }
    return intersections.toArray(new int[0][]);
}